[Excel]Excelの数式と仲良くなりたい人向けの話
2020年4月21日
今回はExcelの数式の話です。これから仲良くなりたい人向けの話です。”数式は苦手だけど日本語なら何とか”って人が対象です。
Excelの数式について実践的な内容を学習したい方は、Excelの生みの親であるMicrosoft社のホームページをご参照下さい。もしくは、GoogleでExcelと検索すると参考になるホームページが無数にヒットしますので、そちらも合わせてご参照下さい。
はじめに
Excelに苦手意識を持っている人の多くは、数式が理解できないことが原因なのかなぁと個人的に思っています。その気持ちはわかります。英語が喋れないのにアメリカ人と友達になれと言われても難しいでしょう。誰かと仲良くなるには、まず相手を知ることから始まります。そのためにも意思の疎通が必要です。しかし、Excelは日本語を覚える気が無いので、我々がExcelの言葉を覚える必要があります。Excelの母国語は機械語ですが、人間とお話するための言葉を2つくらい習得しています。その内の一つが数式です。もう一つはVisual Basic for Applications、略してVBAと呼ばれるものですが、こちらは数式と比較すると少し難解な言葉です。まずは数式から覚えていきましょう。
数式を理解する心構え
数式自体を説明をする前に、数式を理解する上での心構えを説明します。
数式は無理して理解する必要はありません。理解できなかったら一度理解することを止めましょう。
最近は常識と反対のことを唱えて注目させる手法を(私が)良く目にしますが、そういう話ではありません。数式に限らず何でもそうだと思うのですが、興味の無いことは頭に入りません。また、理解に必要な知識を持っていないと頭に入りません。入らないものは無理しても入りませんから、入るタイミングを待ちましょう。幸い、数式が理解できなくても、各所Excel入門サイトで紹介されている数式をセルに貼り付ければ、Excelは動きます(セル参照くらいは編集する必要がありますが)。何度も同じ数式を使用していると、目と頭が数式に慣れてきますし、多分興味も出てきます。慣れてきた所で、改めて数式を理解しようとしてみて下さい。スッと頭に入ってくるタイミングが、必ずあります。数式が難しいと感じるのは、まだ頭に受け入れる準備が無いだけなので、理解できなくても気にせず数式をコピペしてExcelを活用して下さい。数式が理解できないからといってExcelを使わないと、いつまでたっても数式は理解できるようになりません。まずはExcelを使いましょう。
数式とは何か?
改めて、数式とは何でしょうか?定義から確認していきましょう。
数式とは、「数・量を表す数字・文字などを記号で結びつけ,数学的な意味をもつようにしたもの。式。」です(weblio辞書より引用)。
分かり難いですね。一番身近な数式は、学校の算数や数学の授業で書いていた計算式のことです。算数の場合、「1+1」、「2×3」又は「4÷5」などです。数学の場合、ここに変数や関数(sin , cos , log , ∫, etc)などが加わります。ここで、数学が苦手だからExcelも無理だと思わないで下さい。数学は理論重視ですが、Excelは実務重視です。Excelはあなたに難解な証明問題の解答を求めたりしません。Excelはむしろ面倒な計算を肩代わりしてくれます。算数や数学の場合、数式を紙に書いても、眺めているだけでは答えが浮き出てきたりしませんが、Excelならセルの中に数式を書くだけで、勝手に数式を計算して答えを表示してくれます。Excelを手に入れた瞬間とは、人間が小難しい計算から開放された瞬間です。素晴らしいですね。どれくらい素晴らしいかというと、私は自力で計算を一切しなくなり、会社の昇格試験で久しぶりに簡単な計算問題を解いた際、計算速度が劇的に遅い上、割り算の筆算のやり方を完全に忘れてしまうほど依存するくらいには素晴らしいです。ちなみに昇格試験では、何とか捻り出した答えも合っているかどうか不安で、何度も再計算しました。感覚としては、車に乗り始めてから自転車に乗ることが無くなり、数年ぶりに自転車に乗ってみたらスゴク怖かった感覚に似ています。
閑話休題。Excelの素晴らしさが伝わった所で、数式の話に戻ります。Excelの数式も、本質的には算数や数学の数式と同じものです。ただ、この数式をExcelに解いてもらうために、Excelの都合に合わせた書き方をする必要があるだけです。具体的には、数式は紙ではなくセルの中に書く、数式の先頭に必ず「=」を付ける、算数の「×」は「*」(アスタリスク)に、「÷」は「/」(スラッシュ)に置き換える等です。このようなルールは、こういうものだと暗記しましょう。理不尽に感じる人もいるかもしれませんが、視点を変えてみれば、数学の「+」を、なぜ「+」と書くかを説明された人、又は説明できる人は少ないでしょう。別に数式は「1足す1」でも「add 1 , 1 」でも良いと思いませんか?実は、そういうルールで計算すると決めて(定義して)しまえば、それでも良いのです。数学も、足し算の記号に「+」を使うと定義しただけです。Excelも同じく、Excelの開発者が掛け算の記号に「*」を使うと定義したのです。やろうと思えば、例えば”黒箱電卓”というソフトを開発して、加算するための記号を「あばばばば」と定義してしまうこともできます。黒箱電卓において、「1あばばばば1」の答えは2です。調子に乗って、数の「1」を「黒」、「-1」を「箱」と定義しましょう。「黒あばばばば箱」は「0」ですね。ただ、誰もこういうことをしないのは、加算記号や数値を改めて別の言葉で定義することに理論性や合理性などのメリットが無いためです。「1+1」は義務教育修了者であれば常識として誰でも理解できますが、「1あばばばば1」はこの記事を読んだ人しか理解できません。理解してもらうためには教育が必要です。教育にはコストが掛かります。そのコストを支払ってでも常識と異なる定義をするのであれば、それなりの理由があるのです。その理由を理解することは知的好奇心を満たすことくらいには役立ちますが、目の前のルールや現実を変える力は無いので、数式の書き方は暗記してしまう方が時間の節約になります。それに、嫌になるほど数式を書いていると、決められたルールの背景を何となく想像できるようになってきます。
では、黒箱電卓を例にして改めてもう一度数式の定義を読んでみましょう。数式とは、「数・量を表す数字・文字(1,2,黒,箱など)を記号(あばばばば)で結びつけ,数学的な意味をもつ(計算できる)ようにしたもの。式。」です。
何となく数式というものが掴めましたでしょうか?
数式の構成要素
数式の定義が何となく理解できたところで、Excel数式の構成要素について説明します。Excel数式の構成要素は定数、演算子、セル参照又は関数のいずれか又は全てになります。
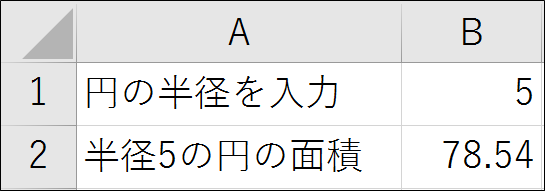
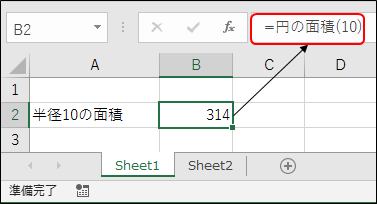
例として、B1セルに円の半径を入力すると、その面積を算出する数式を考えます。円の面積は「半径の2乗×円周率(3.14)」でしたね。下記の例では、B1セルに円の半径として定数5を入力しています。入力に対して、B2セルに円の面積が表示されていますね。よく見ると、A2セルに表示されている説明文に「5」という数字が入っていますね。手入力した訳ではありませんよ?
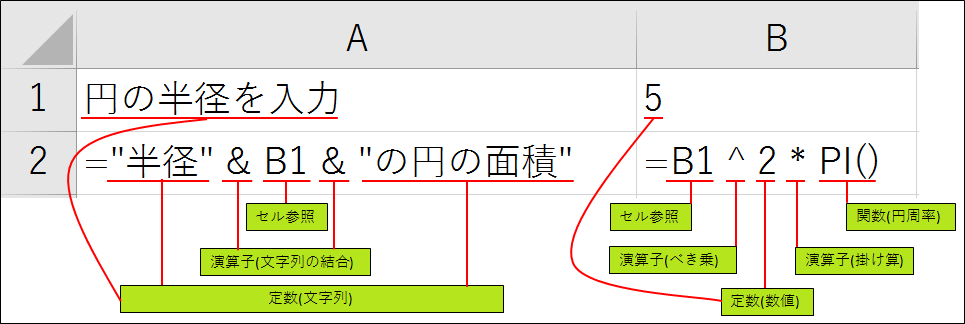
数式を表示してみると、下記のようになっています。Excelの数式は、どんなに複雑なものでも、この4つの組み合わせです。理解したいけど理解できない数式に出会ったら、数式を分解してみましょう。全てを理解できなくても、得るものはあるはずです。
さて、数式の4つの構成要素について詳細な説明をする流れですが、定数、演算子及びセル参照でつまづく人は少ないかなぁと個人的に思っているので、これらは簡単に説明します。
定数
定数とは、数式に直接入力された数値や文字などのことです。定数と書いておきながら、文字列も定数と呼びます。コンピューターから見れば文字列も数値の羅列なので正しい表現なのですが、世間一般の人が聞くと違和感がありますね。Excelの場合、数式内に文字列定数を書く場合、文字を「"」(ダブルクオーテーション)で囲みます。何でかというと、入力した文字が文字列定数であることをExcelに伝えるためです。きちんと伝えないと、Excelは入力された文字を他の数式の構成要素(演算子、セル参照又は関数)のいずれかが入力されたと判断してしまいます。特に、Excelで「名前の定義」という機能を使えば、セル参照に任意の名前を付けられます。例えばB1セルに「半径」という名前を付けることができるので、数式内に「半径」という単語があったとき、Excelからしてみれば、セル参照なのか文字列なのか区別が付きません。区別するために「"」が必要なのです。
演算子
演算子とは、計算式に使う記号のことです。具体的には、+、-、*、/、<、>などです。列挙したとおり、算数や数学の授業で慣れ親しんだ記号が多いことから、大半は直感的に理解できるでしょう。たまに見慣れない記号も出てきますが、数は少ないので、そのような演算子に直面した時に調べれば十分です。
参考までに、Excelで使用できる演算子をMicrosoftのホームページから引用してきたものを載せておきます。この場で全部覚えるのではなく、必要性を感じた時に、必要なものを覚えましょう。
|
算術演算子 |
説明 |
例 |
| + (正符号) | 加算 | 3+3 |
| – (負符号) | 減算
負の数 |
3-1
-1 |
| * (アスタリスク) | 乗算 | 3*3 |
| / (スラッシュ) | 除算 | 3/3 |
| % (パーセント記号) | パーセント | 20% |
| ^ (キャレット) | べき算 | 3^2 |
比較演算子
|
比較演算子 |
説明 |
例 |
| = (等号) | 左辺と右辺が等しい | A1=B1 |
| > (より大記号) | 左辺が右辺よりも大きい | A1>B1 |
| < (より小記号) | 左辺が右辺よりも小さい | A1<B1 |
| >= (より大か等しい記号) | 左辺が右辺以上である | A1>=B1 |
| <= (より小か等しい記号) | 左辺が右辺以下である | A1<=B1 |
| <> (不等号) | 左辺と右辺が等しくない | A1<>B1 |
文字列連結演算子
| 文字列演算子 | 説明 | 例 |
| & (アンパサンド) | 2 つの文字列を結合、または連結して、1 つの連続する文字列の値を作成する | (“北"&"風") |
参照演算子
| 参照演算子 | 説明 | 例 |
| : (コロン) | セル範囲の参照演算子。指定した 2 つのセル参照と、その間に含まれるすべてのセルによって構成される 1 つの参照を作成する | B5:B15 |
| , (コンマ) | 複数選択の参照演算子。複数の参照を 1 つの参照に結合する | SUM(B5:B15,D5:D15) |
| (スペース) | 共通部分を示す参照演算子。2 つの参照に共通するセル参照を作成する | B7:D7 C6:C8 |
セル参照
セル参照とは、あるセルが持つ値を、別のセル内の数式で使用するための手段です。通常は数式の中に「A1」のようにセルのアドレスを入力することで実現しますが、前述の通り「名前の定義」を使用することで、任意の名前でセル参照をすることもできます。余談ですが、複雑なワークシートを作る場合は、「名前の定義」をフル活用しましょう。数式の可読性が格段に向上します。
サラッと書きましたが、セル参照はセルが持つ「値」を取得するという事実は正しく認識しておくべきでしょう。本筋では無いので詳しくは説明しませんが、Excelのセルは大きく3層構造になっていて、下から順に、数式部、値部、表示部に分かれています。例えば数式部に円周率を返す関数「=PI()」を書いた場合、値部には「3.14159265358979」という数値が入ります。表示部には、セルの書式設定で設定された通りに整形された文字列が入ります。書式設定が「000.000」なら表示部には「003.142」という文字列が入ります。日付の場合、数式部が「=TODAY()」なら値部は(2018年03月31日に実行した場合)「43190」、表示部は(一例として)「2018/3/31」となります。セル参照で取得される値は「43190」という数値です。
関数
みんな大好き関数です。関数を使用することを「関数を呼び出す」と表現することもあります。関数を呼び出すときは、「=PI()」のように関数名にカッコを付けます。
さて、改めて関数とは何でしょうか?例によって定義を確認します。
①〘数〙 〔function〕 二つの変数 x ・ y の間に,ある対応関係があって, x の値が定まるとそれに対応して y の値が従属的に定まる時の対応関係。また, y の x に対する称。この時 x は単に変数または独立変数と呼ばれる。 y が x の関数であることを y=f(x)などと表す。ふつう関数といえば, x の値に対して y の値が一つ定まるもの,すなわち一価関数をさす。従属変数。
②与えられた引数(ひきすう)によって動作を変える,コンピューターのプログラム。表計算ソフトなどでは,定型の計算を行うために使われる。
(weblio辞書より引用)
Excelは表計算ソフトなので、定義としては②の方が適切でしょう。これだけ読んで関数の意味が分かる方はこの記事を読んでいないと思いますので、もう少し解説します。
関数とは、数式に名前を付けたものです。それ以上でも、それ以下でもありません。逆に言えば、名前の付いた数式を関数と呼んでいるだけです。例えば、先の円の面積を求める数式を関数にすることも技術的には可能です(VBAを使います)。なお、本記事を読んでいる皆様は独自の関数を作る必要はありませんし、余程の理由が無い限りは作るべきではないでしょう。しかし、関数というものを理解するために、関数を作る側の立場になって考えてみましょう。
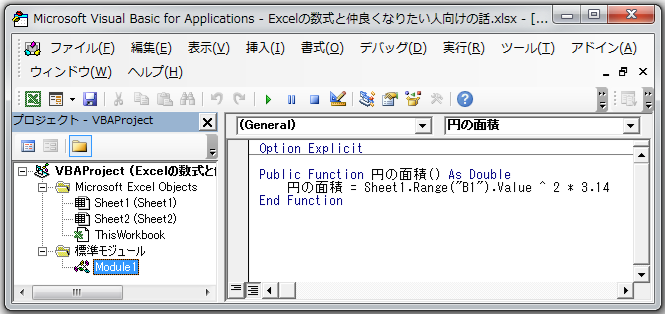
円の面積を計算する関数を考えてみましょう。数式は前述の通り「=B1^2 * PI()」ですが、分かりやすさのために「=B1^2 * 3.14」と書きます。これに名前(関数名)を付けます。関数名は「円の面積」でどうでしょうか?今後は円の面積を求める際、「=円の面積()」と書くだけで任意の円の面積を求めることができます。具体的な計算式を書くよりも、何の計算を行っているか一目瞭然ですね。これは関数を使用する大きなメリットの一つです。
参考までに、この関数は下記のように作っています。(※理解する必要も覚える必要もありません)
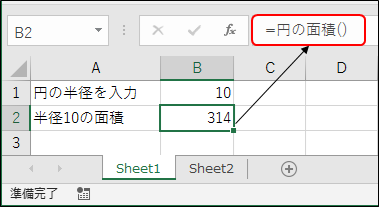
これで、今後は円の面積を求めるときは、この関数が使えますね!試しに、半径10の円と半径20の円の面積を求めてみましょう。関数「円の面積」はB1セルから半径の値を取得しているため、B1セルに10を入力し、適当なセルに「=円の面積()」と入力します。次に、B1セルに20を入力し、・・・と、ちょっと待ってください。B1セルは半径10の面積を求めるために使用中です。B1セルに20を入力したら、半径10の円の面積の結果が表示できなくなってしまいます。・・・困りました。失敗の原因は、「円の面積」関数が、円の半径をB1セルからしか取得できない所にありそうです。そこで、関数内で半径の入っているセル参照を指定するのではなく、関数を呼び出す際に半径の入っているセル参照を指定できると便利そうですね。欲を言えば、セル参照だけでなく、定数も指定したい所です。それを実現するのが引数(ひきすう)です。はい、聞き慣れない単語が出てきたと思って拒否反応を示さないで下さい。簡単な話です。
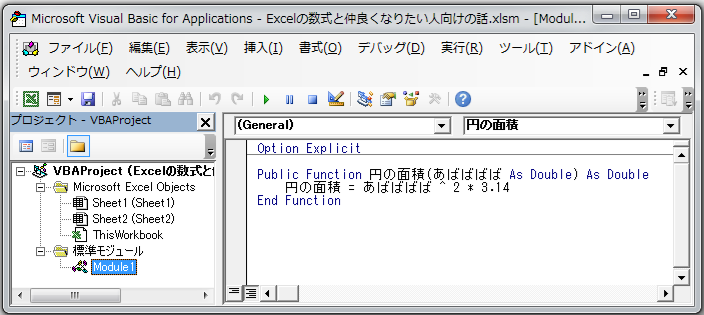
関数を使用する際、個別にセル参照又は定数を指定する関数を「円の面積」関数で考えてみましょう。この関数を数式にすると「=A^2 * 3.14」です。ここで、「A」は半径になります。さて、なぜ「A」が半径なのでしょうか?この「A」は、半径の具体的な数値の代わりに書いた文字です。「A」は私が何となく選んだ記号で、別に「B」でも「半径」でも「あばばばば」でも良いです。この関数を使って半径10の円の面積を求める際は、「=円の面積(10)」と書きます。Excelで実際に使用した例を下記に示します。
ちゃんと計算できてますね。
参考までに、この関数は下記のように作っています。(※理解する必要も覚える必要もありません)
この「A」でも「B」でも「半径」でも「あばばばば」でも良い、数値の代わりに書いてある文字を引数(ひきすう)と呼びます。関数を作成する際、数式の中で具体的な値を決められないものが引数となります。なお、関数を呼び出した結果、関数から得た値のことを戻り値(もどりち)と呼びます。戻り値を得ることを”関数が戻り値を返す”と表現することもあります。「円の面積」関数を例にすると、”「円の面積」関数の引数あばばばばに10を与えると、戻り値314を返す”と言います。
さて、ここまで理解した上で、改めて関数の定義②を読んでみましょう。
②与えられた引数(ひきすう)によって動作を変える,コンピューターのプログラム。表計算ソフトなどでは,定型の計算を行うために使われる。(weblio辞書より引用)
なんとなく理解できましたでしょうか?何となく分かれば十分です。
最後に
いかがでしたでしょうか?今回は実務的な説明は一切無く、概念的な説明に重点を置いてみました。
最初は数式の文法など、実務的な内容を書こうかと思ったのですが、そのような内容のホームページはMicrosoft社のものを含め、既に無数に存在していますので、私が改めて書く必要は無いかなぁと思いました。それに対し、「そもそも数式とは何か?」ということを解説している人は少ないなぁと感じたため、この記事を書いてみました。想像するに、数式の書き方を覚えれば、暗黙的に理解する内容であるため、言語化される機会が少ないのかなと思います。この記事が、あなたの数式に対する見方を変えるキッカケになれば幸いです。
おまけ
本記事では、”関数は数式に名前を付けたもの”と言いましたが、”Excelの関数が数式で表現できるとは思えない!”と感じている方もいらっしゃるかと思います。念のため、そんな方のためにおまけを用意しました。
突然ですが、Excel関数の代名詞といえばSUM関数でしょう。恐らく知名度No1、使い方も簡単で使用頻度も多く、初めて使った関数はSUMだったという人も多いはず。そんなSUM関数と同じような機能を持つ自作関数を作ってみました。名付けて「黒箱SUM」です。ExcelにSUM関数がある以上、一切実用性の無い黒箱SUMですが、今回特別にその中身を見せちゃいます。
どうぞ!(※理解する必要も覚える必要もありません)
はい、何が書いてあるか良く分からないですね。でもこの黒箱SUM、本家ExcelのSUM関数と同様に、引数で指定した値の合計を返してくれます。
”なんだか数式っぽくない!”と感じた方、良い感性をされています。これは”数式”と呼ぶより”コード”と呼んだほうが適切でしょう。ですが、別に嘘をついた訳ではありません。
Excelに仕事をさせる文章という意味では、数式もコードも本質的な違いはありません。強いて言うなら、書くときのルールが少し違うくらいです。関数の役割は、Excelに仕事をさせる文章に名前をつけて分かりやすくすることです(それだけではありませんが・・・)。なので、記事の中では誤解を恐れずに断定的な言い方をしました。いずれにしても、関数に対する理解が深まれば幸いです。
スポンサーリンク
この記事のトラックバックURL
スポンサーリンク
カテゴリー
スポンサーリンク
-
ホーム -
上へ

ディスカッション
コメント一覧
まだ、コメントがありません